Mathematical methods in physical sciences provide essential tools for modeling and solving complex problems. They bridge abstract mathematical concepts with practical applications, enabling scientists to analyze and predict phenomena across various disciplines. Key resources like textbooks and PDF guides offer comprehensive learning support, making these methods accessible to students and researchers alike.

Importance of Mathematical Techniques in Physical Sciences
Mathematical techniques are fundamental to the physical sciences, providing the tools necessary to analyze and solve complex problems. They enable scientists to model phenomena, make precise predictions, and develop new theories. Differential equations and vector analysis are particularly vital, offering frameworks to describe dynamic systems and spatial interactions. These methods ensure that scientific conclusions are grounded in logical and precise calculations, fostering innovation and reliability in research. Moreover, they serve as a common language across disciplines, facilitating interdisciplinary collaboration. With resources like textbooks and PDF guides widely available, these techniques are accessible to students and researchers, promoting a deeper understanding of physical phenomena and driving advancements in fields such as quantum mechanics and electromagnetism. Ultimately, mathematical techniques are indispensable for advancing our comprehension of the natural world and solving real-world challenges.

Key Mathematical Techniques in Physical Sciences
Key techniques include differential equations, vector analysis, and eigenfunction expansions, which are essential for modeling dynamic systems and spatial interactions in physics. These methods provide precise tools for analyzing and solving complex scientific problems efficiently.
Differential Equations
Differential equations are fundamental tools in physical sciences, enabling the description of dynamic systems and changes over time or space. They are widely applied in fields such as physics, chemistry, and engineering to model phenomena like heat diffusion, fluid dynamics, and population growth. The eigenfunction expansion method is particularly useful for solving partial differential equations (PDEs), which often arise in quantum mechanics and other advanced applications. These equations provide a mathematical framework for understanding rates of change and predicting system behaviors. Resources such as textbooks and PDF guides offer detailed explanations and problem-solving techniques, making differential equations accessible to students and researchers. By mastering these methods, scientists can analyze complex systems and derive precise solutions to real-world problems. The ability to formulate and solve differential equations is a cornerstone of theoretical and applied physical sciences, underpinning advancements in technology and scientific discovery;
Vector Analysis
Vector analysis is a cornerstone of mathematical methods in physical sciences, providing tools to describe and analyze quantities with both magnitude and direction. It is essential in fields like electromagnetism, fluid dynamics, and quantum mechanics. Key concepts include vector spaces, dot products, cross products, and gradient, divergence, and curl operations. These methods enable the manipulation of vector fields, which are crucial for understanding physical phenomena such as electromagnetic waves and fluid flow. Resources like textbooks and PDF guides offer detailed explanations of vector calculus, including practical applications and problem-solving techniques. By mastering vector analysis, scientists can model complex systems and derive precise solutions to real-world problems. Its applications are vast, ranging from engineering to theoretical physics, making it an indispensable skill for any student in the physical sciences. The ability to work with vectors and tensor fields is fundamental for advancing scientific knowledge and technological innovation.

Applications of Mathematical Methods in Physical Sciences
Mathematical methods are pivotal in quantum mechanics and electromagnetism, enabling precise modeling of physical phenomena. Techniques like eigenfunction expansion solve Schrödinger equations, while vector analysis aids in electromagnetic field theory, illustrating their broad applicability in scientific research and problem-solving.
Quantum Mechanics
Quantum mechanics heavily relies on mathematical methods to describe the behavior of particles at the atomic and subatomic level. The Schrödinger equation, a fundamental differential equation, is central to understanding wave functions and probability densities. Mathematical techniques such as eigenfunction expansion and operator theory are essential for solving these equations. These methods enable physicists to model quantum systems, predict energy levels, and analyze transitions between states. The application of mathematical tools in quantum mechanics has led to groundbreaking discoveries, including the behavior of electrons in atoms and the properties of photons. PDF resources and textbooks provide detailed derivations and applications of these methods, serving as invaluable resources for students and researchers. By mastering these mathematical approaches, scientists can deepen their understanding of quantum phenomena and advance theoretical and experimental research in the field.
Electromagnetism
Electromagnetism is a cornerstone of physical sciences, and its analysis relies heavily on mathematical methods. Maxwell’s equations, formulated using differential equations and vector calculus, govern the behavior of electric and magnetic fields. These equations are solved using techniques such as separation of variables and integral transforms, which are detailed in resources like “Mathematical Methods in the Physical Sciences” and other PDF guides. Applications of these methods include modeling wave propagation, understanding electromagnetic induction, and analyzing field distributions in complex media. The mathematical framework of electromagnetism has enabled technologies like antennas, motors, and communication systems. By mastering these techniques, physicists and engineers can solve real-world problems involving electromagnetic phenomena. Textbooks and online resources provide thorough explanations and examples, making these advanced mathematical tools accessible to learners at various levels of study.
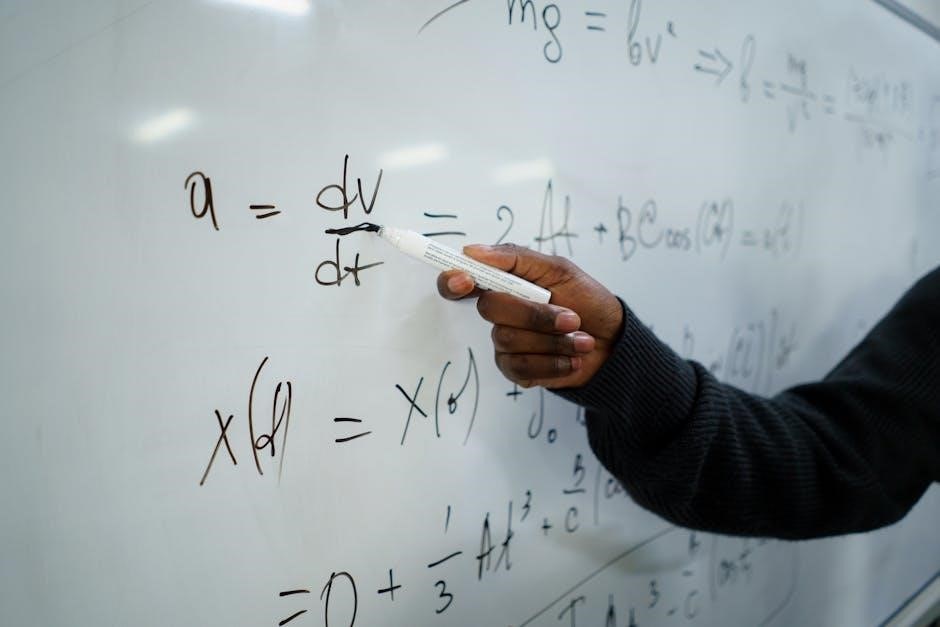
Educational Resources for Learning Mathematical Methods
Textbooks and PDF resources are vital for mastering mathematical methods in physical sciences. Titles like Mathematical Methods in the Physical Sciences, 3e, by Mary L. Boas, and guides by Shawn D. Ryan offer comprehensive learning tools. These materials provide detailed explanations and practical examples, aiding students and professionals in understanding complex concepts and their applications.
Textbooks and PDF Resources
Several textbooks and PDF resources are available for learning mathematical methods in physical sciences. One of the most popular is Mathematical Methods in the Physical Sciences, 3e by Mary L. Boas, which covers essential topics like differential equations, vector analysis, and complex variables. Another valuable resource is Mathematical Methods for Physicists by George B. Arfken, which provides detailed explanations and practical examples. Additionally, Mathematical Methods for the Physical Sciences by Shawn D. Ryan offers a comprehensive two-semester course structure. Many of these textbooks are available as PDF downloads, making them easily accessible for students and researchers. These resources often include problem sets, solutions, and appendices with summaries of key concepts. They are designed to cater to students with a calculus background, helping them develop a strong foundation in mathematical techniques. Online platforms also provide supplementary materials, such as lecture notes and guides, to enhance learning. These resources are indispensable for mastering the mathematical tools required in physical sciences.
